nyx | 2023-10-17 02:42:31 | ⭐️ 1 | 💬️ 2

nyx

T1上机题目思路分享

Verilog向量点乘

题面简述

两个位宽为 32 的 wire 型变量来表示两个需要点乘的 32 维向量，每一位只能是0或者1，输出点乘的结果。

思路分析

比较容易，实际上就是将两个wire型变量的各位进行&操作，再将得到的结果各位相加；当然，更容易想到的应该是直接对比两个输入的各位即可。

部分代码实现

integer i;
always @(*) begin 
//do something
    for ( i = 0; i < 32; i = i + 1) begin
        if (vector_a[i] == 1 && vector_b[i] == 1) begin
            //add one to your register
        end
    end
end

当然可以先进行&运算在相加，不过感觉并没有太大优势（？）

注意事项&&反思总结

1、always并不是只能运用于时序逻辑电路中，always@(*)就可以运用于组合逻辑中

2、寄存器跟C语言中的数组有些类似（更像python），可以通过调用数组名[x:y]调用一个模块

3、循环的使用和C很相似，但是值得注意的是没有i++,自增自减要用i=i+1 、i=i-1

4、注意每次使用的时候寄存器要清零！

Verilog 涂色方案

题面简述

使用R、G、B三种颜色涂色，要求：同一颜色不得连续出现三次，红色不得与绿色相连。

clk上升沿一个颜色代号：0（红色）、1（绿色）、2（蓝色）。设计 Moore 状态机检测该涂色序列的合法性，并在检测到不合法的序列之后将输出端口 check 置为 1。

另外，在检测到不合法序列之后，将最近的一次涂色擦除，重新涂色。

思路分析

题目要求用有限状态机来实现，最直接想到的一般是用define/parameter之类的语句利用status实现，这当然是一种十分通用的解法，我们可以这样子来列状态表：

因为考虑到我们最重要的是判断涂色是否不符合，所以只要重点关注可能会寄掉的状态来规划状态机状态就行，如下是一种方法：

颜色状态	编码
Empty	3'b000
Red	3'b001
Green	3'b010
Blue	3'b011
RedRed	3'b100
GreenGreen	3'b101
BlueBlue	3'b110

使用三位的寄存器即可表示，还是在可以手搓的范围之内。（当然这不是唯一一中的表示方法，比如也可以用两个寄存器，分别表示当前颜色是R/G/B/Empty的哪一种,再来一个寄存器表示出现的次数）各位各显神通即可。

需要注意的是，题目要求用的是Moore,采取这种编码方法需要设置一个寄存器flag来存状态，不然就要用4位的status了。~~（当然不嫌麻烦的可以trytry）~~

状态机转换图所示：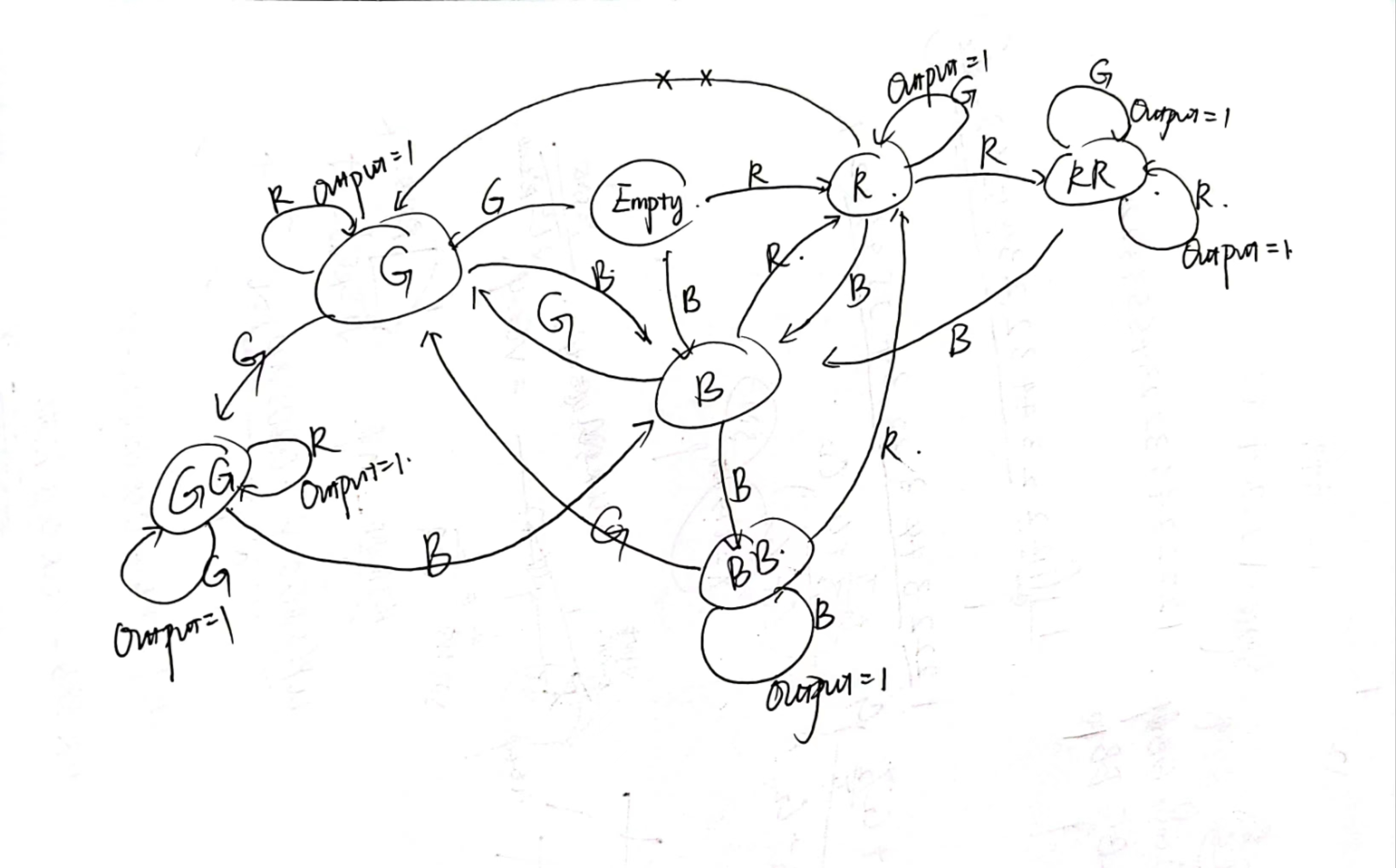

相信大家对于这种基本的格式应该很熟悉了，就不放代码了。但是实际上做题的时候我用的并不是这种方法。我们可以考虑一下C语言中是如何处理这类问题的。大概应该像是这样子的：

	int firstcolor=0;
	int secondcolor=0;//empty
	int nowcolor;
	int check=0;
	//do something
	if(firstcolor == secondcolor && secondcolor == nowcolor){
		check=1;
	}else{
	//other cases 
	}

那我们是不是也可以考虑这样子来实施呢？答案当然是肯定的。我们可以使用两个寄存器first , second存放先前的两个颜色（R/G/B/Empty)，在每次时钟上升沿来临时读入一个新的颜色并且比对：如果坏事了那就check=1,这次不改变first 和 second的值；如果没寄那就把second的值赋给first,再把color赋给second（刚好非阻塞赋值让我们实现了这一点变得很简单）

部分代码实现

reg [1:0] first;
reg [1:0] second;
reg check;
initial begin
    //initial block
end
always @(posedge clk or negedge rst_n) begin 
    if(~rst_n) begin
         //reset
    end else begin
         if (first==second &&second==color) begin
             //do something
             check=1;
         end else begin
             if (/*other wrong cases*/) begin
                 //do something 
                 check=1;
             end else begin
                 //do state transferring
                 check=0;
             end
         end
    end
end

这可比用S0表示status那种方法快多了。这也告诉我们学习不要拘谨于某种固定的舒适圈，走出去看看，外面风景可能更美。（手动狗头）

反思总结

1、区分同步复位与异步复位！！！ 同步复位指的是在clk上升沿来临时，复位信号才有效被读入，也就是说如果不在clk上升沿的reset=1，也屁用没有。

always @(posedge clk or negedge rst_n) begin 
    if(~rst_n) begin
      
    end else begin
        
    end
end//异步复位模板（rst_n低电平有效）

注意到这个信号是negedge rst_n,意味着如果rst_n一直保持0的话也是不会触发这部分条件的。

always @(posedge clk) begin 
    if(~rst_n) begin
      
    end else begin

    end
end//同步复位模板（rst_n低电平有效）

可以看到，两者差别其实只是复位信号是否为always的敏感信号源，仅此而已。

2、尝试走出舒适圈，并不一定要遵循那一套固有模板，现在才P2有试错成本的（再次狗头）。

Verilog 数字掌控领域NumberNest（其实就是特殊的字符串匹配）

题面简述（回忆，应该大差不差）

输入序列一共含有1-5五个数字，每两个相同的数字之间的区域成为掌控领域（原文忘了qwq），如12334421，1的掌控领域为233442,要求进行NumberNest的合法性检查，要求如下:

1、每个数字的掌控领域之内，只能出现比他更大的数字；

2、对于一个合法的序列来说，每一个数字都必须是一个掌控领域的两边组成之一，如121不合法；

3、合法性序列中只能越一级掌控，不能越多级，如12344321合法，而134431不合法；

如果不合法将check置为1,并且将之前的所有输入一锅端清理掉，重新计数，并且数据保证每次开头的数字一定是1。

思路分析

Okay这题我是老老实实的用有限状态机的基本做法实现的，已经跳过一次舒适圈了。最重要的步骤之一就是确定表示什么状态。考虑到输入与之前输出产生联系，用S_i（i=0~5)表示现在位于谁的掌控领域之内,S0与S6表示空与不合法，具体定义如下：

掌控领域	编码	check
Empty	3'b000	0
1	3'b0001	0
2	3'b010	0
3	3'b011	0
4	3'b100	0
5	3'b101	0
WA	3'b110	1

接下来需要确定如何状态转化，这个每个人的理解可能不一样，在此分享我的理解，若有更好的解法希望大佬们能不吝赐教。

对于S_1-5的状态S_i来说，下一位输入的如果是i，那么这个i与先前进入掌控领域状态S_i的那个i相匹配掉了，由于要求3，那么他会返回上一个状态也就是S_i-1;下一位输入的如果是i+1，就进入i的掌控领域之中，状态变为S_i+1；其余输入均是WA,转化为状态S₆并且清理门户，开始新的一轮。

部分代码实现

always @(posedge clk or negedge rst_n) begin 
    if(~rst_n) begin
      //reset
    end else begin
        case(status)
        //previous state
        `S3: 
        if(number==4'b0011) begin
            status<=`S2;
        end else begin
            if (number==4'b0100) begin
                status<=`S4;
            end else begin
                status<=`S6;
            end
        end
        //then S4 and S5
        `S6:
        if (number==4'b0001) begin
            status<=`S1;
        end else begin
            status<=`S6;//若按照题面意思这句话不用写，但其实题目完全可以删掉要求3的保证刚开始输入是1的条件
        end
    end
end

最后当status==S6的时候，check为1 ，结束上机。

反思总结

这一题是非常经典的一道Moore型有限状态机的题目，难度适中。但是我这个笨蛋卡了好久，为什么呢，因为写一堆case中有一个地方打错了导致寄了半个多小时（抱头痛哭qwq),所以大家写case比较多的时候一定要写慢一点、认真检查。

总结陈词

本次主要考察了位运算以及状态机的Verilog实现，难度适中，但是对于我们大部分初学者可能有一定的难度，建议大家还是要加强复习。若有任何问题希望大家斧正，谢谢！

Coooookie（助教）回复 nyx

同学你好，发帖时代码块选择一下代码语言，否则代码没有高亮。

2023-10-17 16:36:19 | CC BY-ND 4.0 ❤️ 0