提示：这篇文章也在作者的博客上发布，协议为 CC BY-NC 4.0。
看上去是没啥用的东西，只是为了满足好奇心 @(o･ｪ･)@
目录
- Sec 1：为何计算校验码需要在数据后补 0？
- Sec 2：为何校验过程恰好整除？
- Sec 3：如何利用校验码进行纠错？
- Sec 4：校验码的并行生成
- Sec 5：Logisim 中 CRC 校验码的生成与纠错
- 参考文献
在 P0 课下中有一道题目，要求我们使用 Logisim 搭建一个除数为 4 位，原数据帧为 8 位的 CRC 校验码计算电路，题目中有提到这样一句话：
因为 B 是 4 位二进制数，我们需要在 A 的后面补上 3 个 0
其中，B 是选定的除数，A 是 8 位原数据。有同学在答疑群中询问这里的因果关系，得知是 CRC 算法规定的的计算步骤，但为何 CRC 算法需要在原数据后面补 0 计算呢？越想越搞不懂，我便上网找了一些资料，并结合自己的推导与概括，和大家分享一下省流版的结论。 (o_O)
约定：此帖所有计算，除非特殊说明，均为模二运算；所有除法，除特殊说明，均为模二带余除法，用 \(r\) 表示余数；所有数字，除特殊说明，均为二进制无符号整数。
Sec 1：为何计算校验码需要在数据后补 0？
先说结论：为了方便校验以及纠错过程[1]。
既然是校验码，肯定是为了防止数据在通信传输过程中出现偏差而诞生的，自然，我们生成的校验码也需要具备校验的能力。
假设通信双方选定一个除数 \(B=1101\)，传输原数据 \(A=1011\ 0010\)。如果不补 0，则有 \(A \divsymbol B = 11001, r = 111\)，将余数拼接到原数据帧后，得到 11 位的输出 \(C=1011\ 0010\ 111\)，接收方接收到数据后，需要将其拆分成 \(8+3\) 位，使用约定好的除数，计算前 8 位的余数，与后 3 位进行比较，从而检验数据传输的可靠与否。
但是，这个过程还是相对繁琐的，也无法判断出错的位置（比如接收到 \(1011\ 0011\ 111\)，余数算下来是 \(110\)，你能知道是数据的最低位传输错误，还是余数的最低位传输错误吗），因此还需要改进。
关于为何这样计算校验码不行，资料 [1] 中仅提到 “过程繁琐”，但我在后续的探求中，觉得这一个观点过于单薄，遂补充了 “无法纠错” 这一原因。
于是，科学家们想出了一种解决方法，就是题目中所描述的那样，在 \(A\) 后补 0，个数为 \(B\) 的位数减去 1，得到 \(A_1=1011\ 0010\ 000\)，此时有 \(A_1 \divsymbol B = 11001101, r=001\)，进行拼接，得到 \(C=1011\ 0010\ 001\)，接收方在接收数据后，计算 \(C \divsymbol B\) 的余数，如果余数是 0，则说明传输过程可靠。
Sec 2：为何校验过程恰好整除？
上述所说并非巧合，补 0 的逻辑也在这里呈现[2]。
不过首先，得引入一个叫做 生成多项式 的东西，对于一个二进制数 \(\overline{d_{n-1}d_{n-2}\cdots d_1d_0}\)，其中 \(d_i=0|1\) 且 \(d_{n-1} \neq 0\)，有唯一的 \(n-1\) 次多项式与之对应：
\[D(x) = d_{n-1}x^{n-1} + d_{n-2}x^{n-2} + \cdots + d_1x + d_0\]
反之亦然。
对于 \(n\) 位的原始数据 \(A=\overline{d_{n-1}d_{n-2}\cdots d_1d_0}\)，以及 \(k\) 位的除数 \(B=\overline{g_{k-1}g_{k-2}\cdots g_1g_0}\)，它们的生成多项式分别为：
\[D(x) = d_{n-1}x^{n-1} + d_{n-2}x^{n-2} + \cdots + d_1x + d_0 \qquad G(x) = g_{k-1}x^{k-1} + g_{k-2}x^{k-2} + \cdots + g_1x + g_0\]
将 \(D(x)\) 两边同时乘以 \(x^{k-1}\)，即添了 \(k-1\) 个 0：
\[x^{k-1} \cdot D(x) = d_{n-1}x^{n+k-2} + d_{n-2}x^{n+k-3} + \cdots + d_1x^k + d_0x^{k-1}\]
对其作多项式的带余除法，得到次数最高为 \(k-2\) 次的余数多项式 \(R(x)\) 与商多项式 \(Q(x)\)：
\[x^{k-1} \cdot D(x) = Q(x)G(x) + R(x)\]
两边同时加上 \(R(x)\)，因为是模二运算，有 \(R(x) + R(x) = 0\)：
\[x^{k-1} \cdot D(x) + R(x) = Q(x)G(x)\]
因为二进制数与生成多项式的一一对应关系，有 \(R(x) = r_{k-2}x^{k-2} + \cdots + r_1x + r_0\)，于是：
\[Q(x)G(x) = d_{n-1}x^{n+k-2} + \cdots + d_1x^k + d_0x^{k-1} + r_{k-2}x^{k-2} + \cdots + r_1x + r_0\]
其对应的二进制数为：
\[C = \overline{d_{n-1}d_{n-2}\cdots d_1d_0r_{k-2}r_{k-3}\cdots r_1r_0}\]
这不是巧了不是，恰好是原数据拼上余数！而且它的生成多项式还恰好等于 \(Q(x)G(x)\)，这也意味着整除！(◆゜∀゜）b
Sec 3：如何利用校验码进行纠错？
通过一些科普性质的文章，我了解到，CRC 校验码可以对一位错的情况就行纠错（也就是，不仅可以判断数据传输的可靠性，还可以把出错的那一位揪出来），其方法是，通过余数（这里的余数指接收方对接收到的数据（包含数据位与校验位）进行模二除法得到的余数）与出错位一一对应的关系查表。
那其中究竟是怎样的一个对应关系呢？
以下过程并不保真，请注意甄别。
首先假设校验位不会出错，且在数据位中有一位错。假设 \(d_s\) 在传输过程中出现差错，则有接收到的 \(C' = \overline{d_{n-1}\cdots d_s' \cdots d_0r_{k-2}r_{k-3}\cdots r_1r_0}\)，其中 \(d_s \oplus d_s' = 1\).
考虑它们的生成多项式与模二加法的性质，则有：
\[C'(x) = C(x) + x^{s+k-1} = Q'(x)G(x) + R'(x)\]
\(R'(x)\) 是校验时得到的余数多项式。又因为 \(C(x) = Q(x)G(x)\)，所以：
\[x^{s+k-1} = (Q(x) + Q'(x))G(x) + R'(x)\]
即二进制数 \(\overline{100\cdots0}\)（\(s+k-1\) 个 0）除以 \(B\) 的余数，就是校验时得到的余数！
拿题目的背景试一试吧！有 \(k=4\)，数据位数为 8.
| 数据位出错位数 \(s\) | \(s+k-1\) | 余数 | 备注 |
|---|---|---|---|
| 0 | 3 | \(101\) | \(1000 \divsymbol 1101\) |
| 1 | 4 | \(111\) | \(10000 \divsymbol 1101\) |
| 2 | 5 | \(011\) | \(100000 \divsymbol 1101\) |
| 3 | 6 | \(110\) | \(\cdots\) |
| 4 | 7 | \(001\) | \(\cdots\) |
| 5 | 8 | \(010\) | \(\cdots\) |
| 6 | 9 | \(100\) | \(\cdots\) |
但是，第 7 位却让我心凉了半截：余数是 \(101\)！这还怎么检错呢？
正当我对上述过程产生怀疑，并准备另找出路时，我突然意识到，余数总共就 3 位，最多 8 种状态，还要把全 0 留给正确的情况，怎么可能完美地纠错呢？
换一句话说，题目给定情况下，余数位数过少！
那还是采用一种主流的位数来讨论吧，数据位数为 4，除数位数也为 4，总数据位数为 \(4 + 3 = 7\).假设取定除数 \(B=1101\)，并且含校验位数据只有一位错，则出错位数与余数的对应关系如下：
| 数据位出错位数 \(s\) | 余数 | 备注 |
|---|---|---|
| 0 | \(001\) | \(1 \divsymbol 1101\) |
| 1 | \(010\) | \(10 \divsymbol 1101\) |
| 2 | \(100\) | \(100 \divsymbol 1101\) |
| 3 | \(101\) | \(\cdots\) |
| 4 | \(111\) | \(\cdots\) |
| 5 | \(011\) | \(\cdots\) |
| 6 | \(110\) | \(\cdots\) |
这样，对于接收方来说，收到 7 位数据 \(C'\)，计算 \(C' \divsymbol B\) 的余数，若余数为 0，则表示没有错误，否则，出错位可按上表查询。
这是一位错的情况，对于两位错，CRC 也同样可以判断（也许需要增加一个奇偶校验位，这里我没有深究），但是无法纠错。对于三位错，CRC 就无能为力了，当然，这种情况极其罕见。
Sec 4：校验码的并行生成
通过一些科普性质的文章，我也了解到，CRC 校验码的生成还有一种并行的方法，就是将若干个数异或起来得到余数。
假定 \(A=1011\)，\(B=1101\)，给定一个原始串 \(C_0=0000\ 000\)，这是 CRC 校验成功的。现在，使其逐位接近 \(A\)，有第 6、4、3 位的差异，那么将这些位上对应的余数异或起来，可以得到 \(C = 1011\ 100\)，这就是生成好的 CRC 校验码。
我觉得整个过程可以理解为纠了三次错，从 \(0000\ 000\) 纠正到了 \(1011\ 100\).
那么，校验的过程是不是也可以并行执行呢？应该也是可以的，不赘言。
Sec 5：Logisim 中 CRC 校验码的生成与纠错
总要写一点和课程相关的内容的吧 ᕕ( ᐛ )ᕗ
按照上面的思路，对于 \(B=1101\) 的情况，结合余数表，可以很容易画出如下的电路：
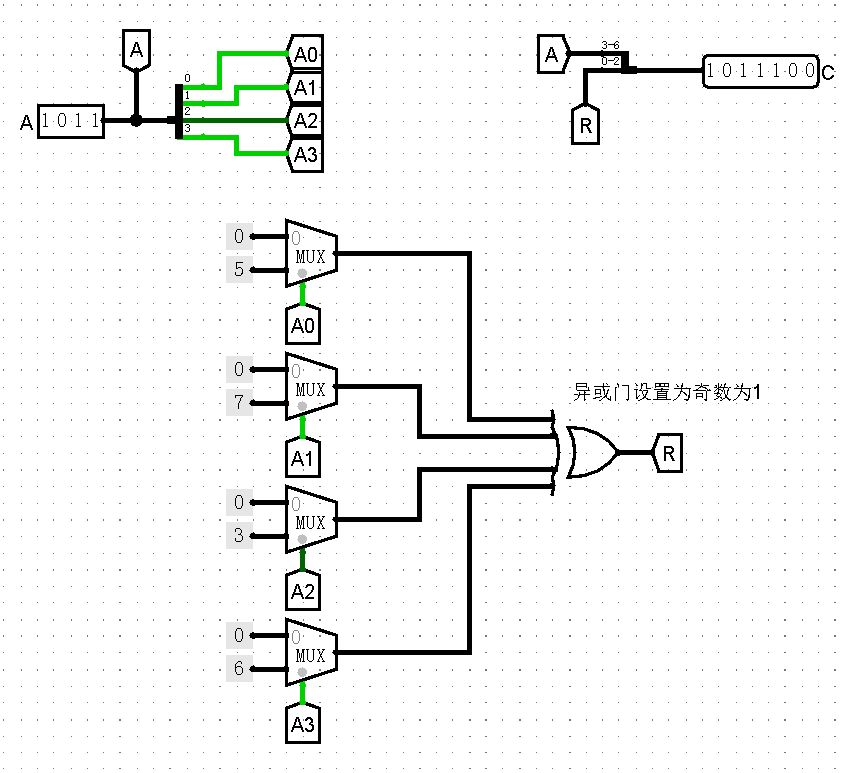
此外，我还弄了一个简单的测试电路，将其结果与使用模二除法得到的结果进行比较，如下分别是数据设置与比较电路：
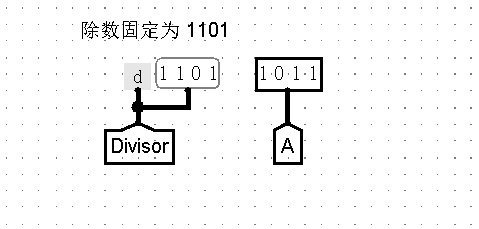
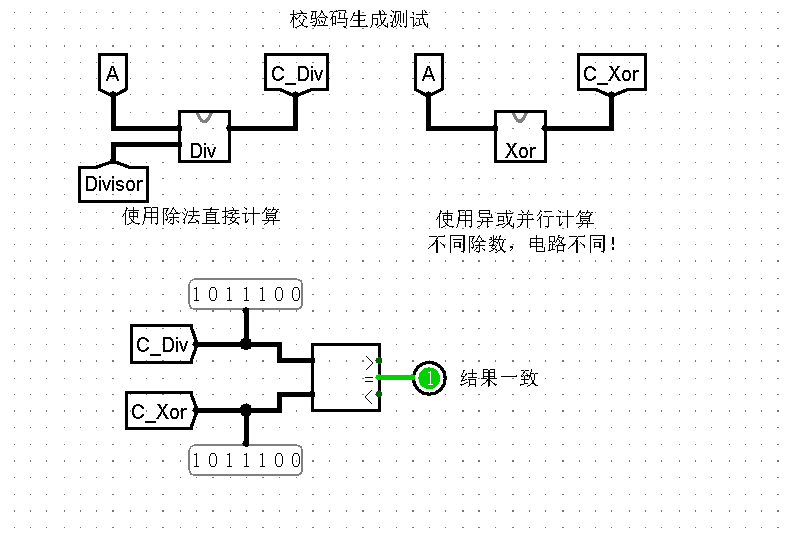
对 CRC 校验码进行一位纠错也很简单，这里采用除法简化过程（好像有个类似的并行的纠错电路，但是研究不动了 (．． )…）
如下是扰动设置与余数表的生成电路：
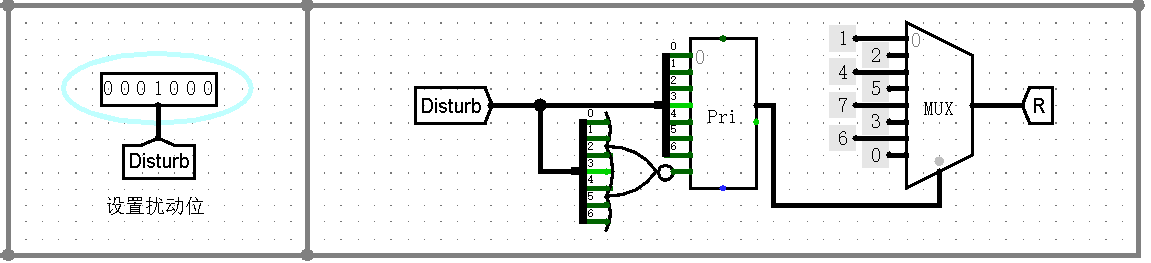
并通过 7 位除法得到校验余数：
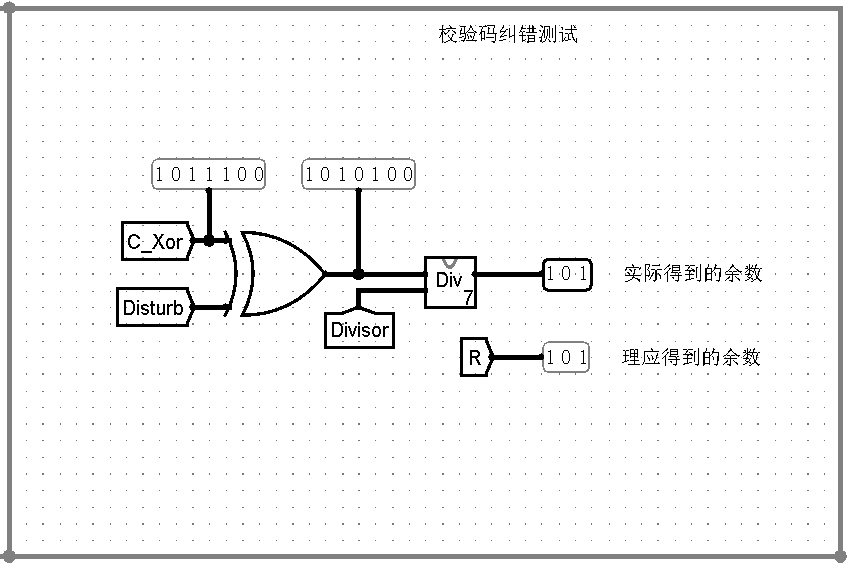
这里并没有真正得到纠错后的数据，但只要将得到的余数与余数表比较即可！
什么？你在说 P0 课下那道题？拜托，那个题很不一样的好吗，算 8 次除法得了，而且除数还不确定 ……
参考文献
[1] 思否论坛.不要跑，CRC没这么难！（简单易懂的CRC原理阐述）[EB/OL].(2019-02-02)[2023-09-28].https://segmentfault.com/a/1190000018094567（存档）
[2] 仇晓涛.通用并行CRC计算方法及FPGA实现[J].无线互联科技,2023,19(02):115-117+168.