提示：这篇文章也在作者的博客上发布，协议为 CC BY-NC-ND 4.0。
十分侥幸地通过了P0，但也暴露了许多问题，于是和几位同学讨论反思后做一些记录，希望对自己对大家能够有所裨益，为接下来的P3做一点准备~
本文中展示的方法仅为我和一些同学的做法，无法代表大多数人的思路。如大家发现错误或不严谨处，请务必不吝加以斧正！
鸣谢：朱雄伟（T1五线谱作者）
廖鹏飞（手点2^12真值表一次过）
卞卓航（狠狠学习了）
魏新明（思路打开）
T1：P0_L2_nonexist_2023
未出现的正整数 题目编号 1120-1149
题解：
这道题初看时曾经以为是算法题或者位运算题，经过思考排除了这两种可能
本题有两种常见的做法，直接比较（较简单）和排序判断（较繁琐）
比如我的狠人舍友，选择了排序判断（最有勇气的一集）
直接比较
根据抽屉原理，由于无符号数只有5个，本题的最终答案只可能在1~6范围内（最关键一步），想到这一点后，电路的搭建就十分清晰了
1.依次判断出数1~5在所给的无符号数中有没有出现
这部分可以使用比较器和门电路等器件方便地得出结果
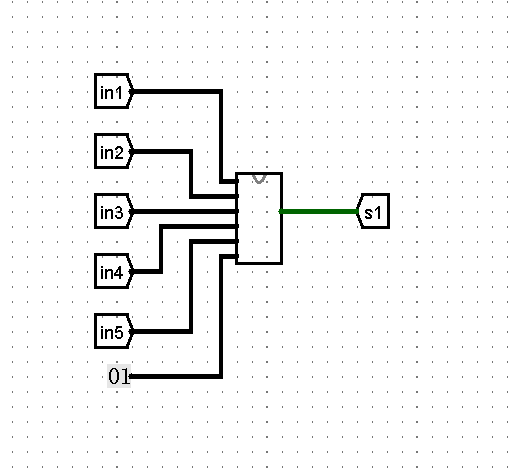判断电路(1/5)(已隐去部分电路细节)
2.通过组合逻辑分析或位运算等方式求出最小未出现的正整数
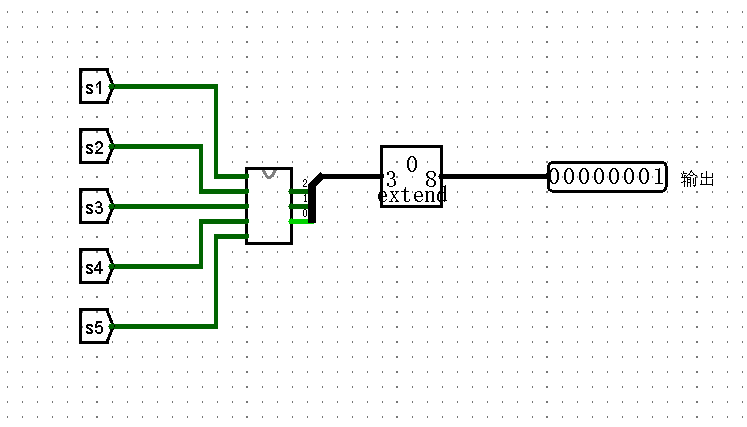输出电路(已隐去部分电路细节)
Tips：
- 建议将比较器的判断类型调为unsigned，和题目所给数据一致
- 题目要求输出8位二进制数，若位数不满，则需要bit extender拓展
- 记得调appearance!!记得调appearance!!记得调appearance!!
排序比较
本来是没有这部分的，但出于对我舍友的尊敬，经过他本人同意，将他的做法展示于此
1.将5个数进行冒泡排序
在之前的学习中，大家学习了多个数进行排序输出的方法，本题也可以如此操作：先抽象出一个两个数间排序的模块，再按照冒泡排序的方法对5个数排序
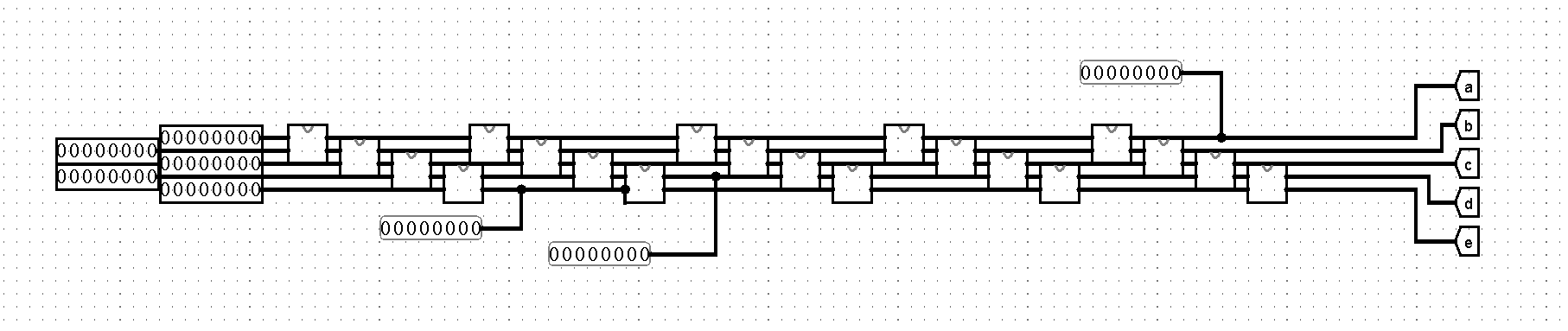排序电路——我愿称之为五线谱
2.判断哪两个数之间存在没有出现的正整数
将排序好的五个数两两间做差（第一个数和0做差），若某个差大于1，则说明在这两个数之间有没有出现的正整数
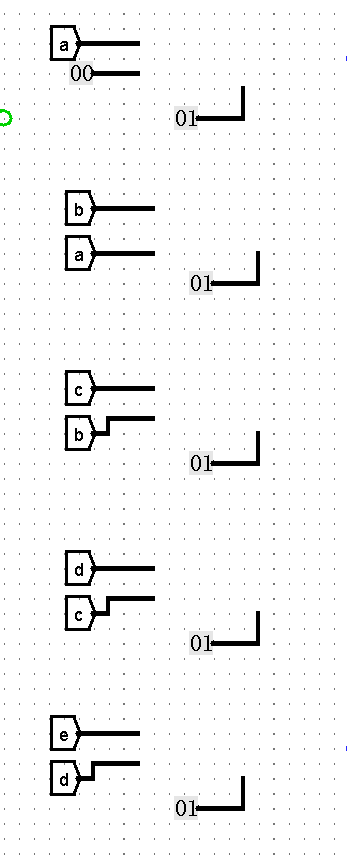判断电路(已隐去部分电路细节)
3.输出所求正整数
通过组合逻辑得到差值大于1的两个数中最小的一对，答案即为较小数+1，可以使用MUX来简化电路
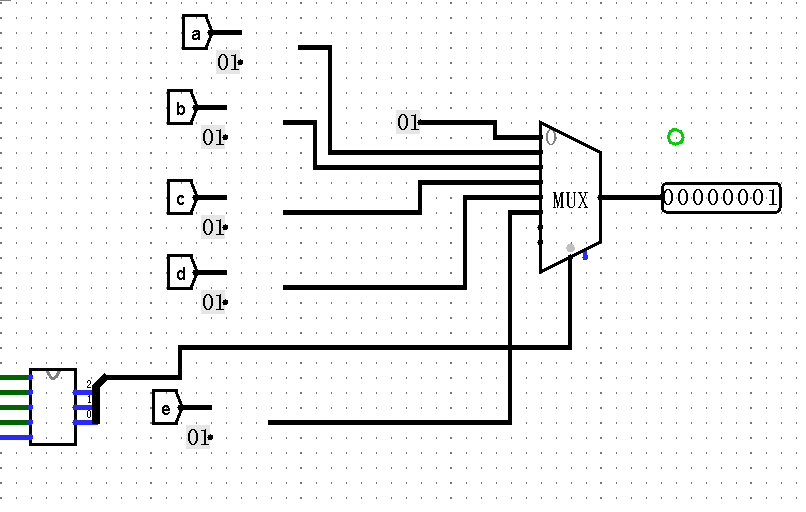输出电路(已隐去部分电路细节)
T2：P0_L3_walker_2023
回字楼游走 题目编号 1120-1158
题解：
题目十分类似课下的navigation题，画出状态转换图、列出真值表、搭建标准电路，就能够解决（留了个超链接，方便大家回顾www）
需要注意的地方有两点：
题目默认房间号为1-8，但假如直接这样子打表的话需要四位来存储房间，为了简化可以规定房间号默认减一为0-7，这样只需要三位就可以存储了，可以省下50%的打表时间（最后答案别忘了用一个mux或者加一）。
我下图的状态机和电路也采用了这种优化~
记得调appearance!!记得调appearance!!记得调appearance!!
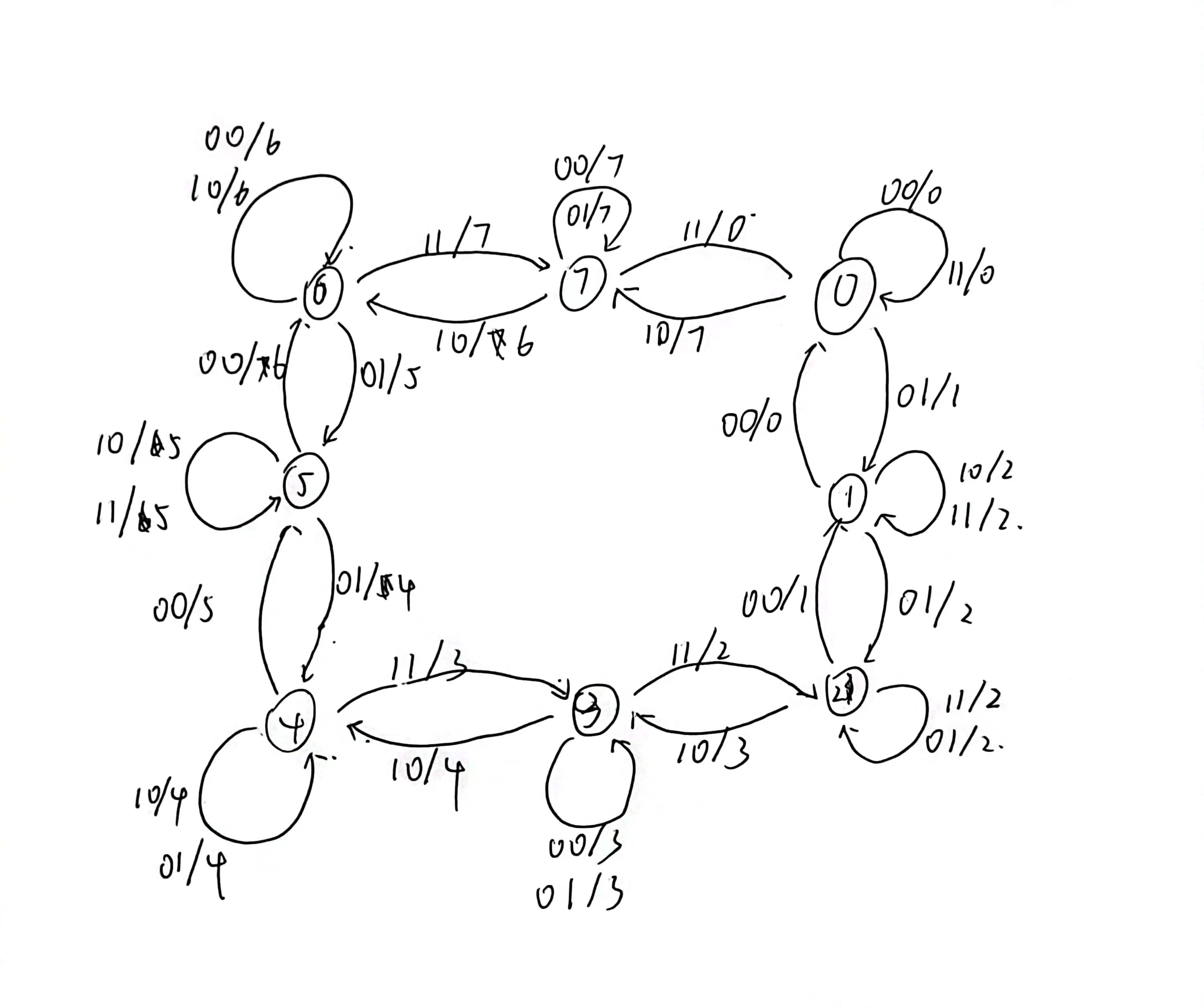考试中所画状态机
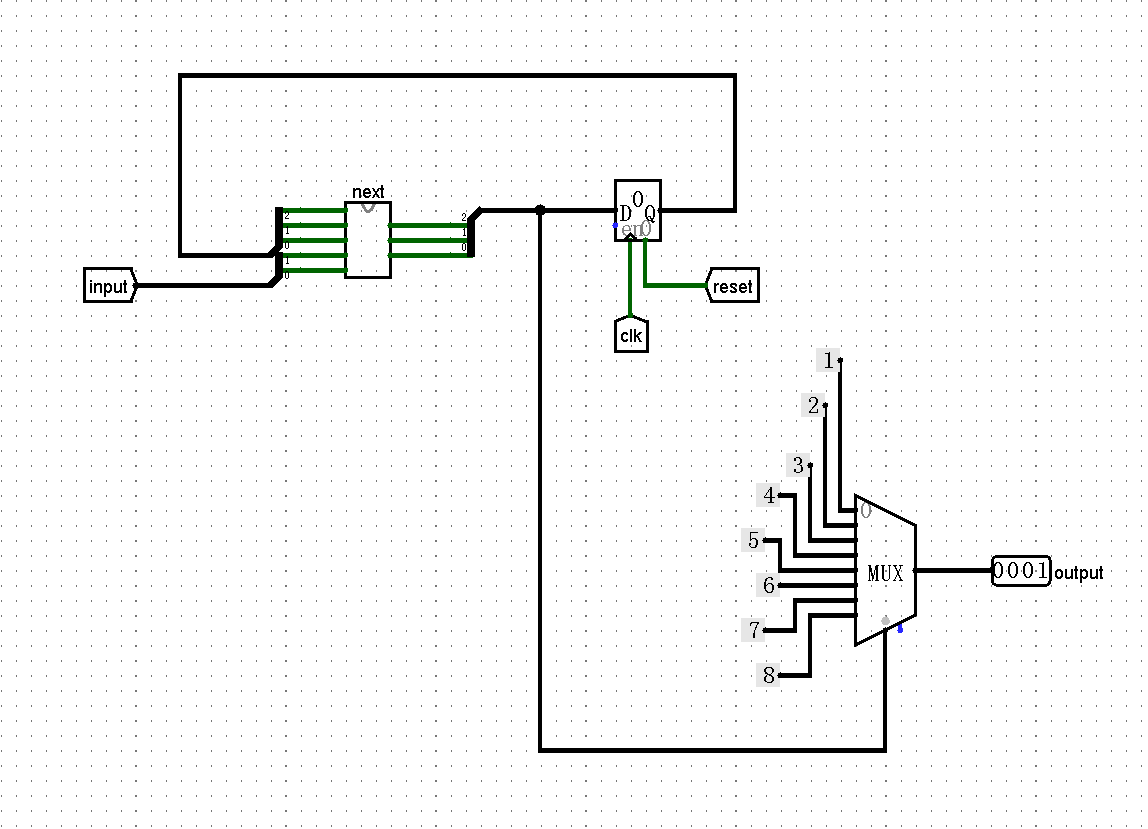主电路
T3： 十六进制数匹配
题意：
串行输入一个4位数，根据之前输入的三个4位数按要求输出：
- 若三个数为A0E，输出01
- 若三个数为EEE，输出10
- 若三个数为0A0，输出11
- 若都不满足，输出00
因为题目有些忘了，输出的数据可能顺序不对，请大家谅解www
题解：
法一
整体思想为通过寄存器来维护之前读入的三个4位数（状态），每个周期通过组合逻辑判断输出，形成一个样子不是很标准的状态机
使用三个寄存器维护状态
每次状态转移时都进行如下操作： \[ in\rightarrow reg1\rightarrow reg2\rightarrow reg3 \] （类比移位寄存器，但每次移4位）
注意：这部分也可以使用一个12位寄存器或者RAM来解决
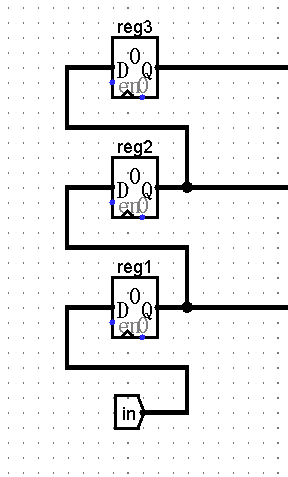状态转移电路
使用组合逻辑分析判断答案
创建三个模块cirA0E,curEEE,cur0A0，分别判断是否满足A0E,EEE,0A0的条件（满足输出1，不满足输出0），最后哪个亮了输出哪个
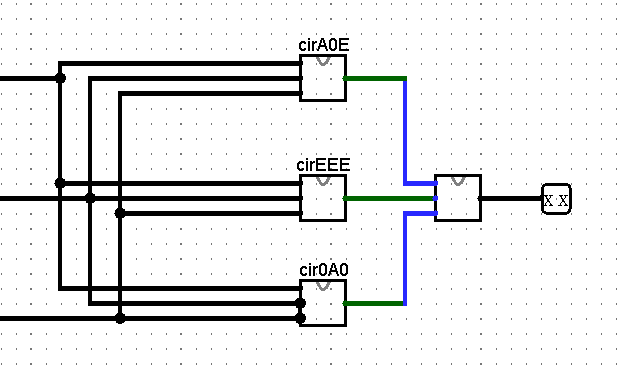输出电路(ver 1.0)
3.添加counter
上面的电路虽然看起来完善了，但是提交后并不能够通过
注意到题面中有一个要求的序列为0A0，当我们reset后输入A0时，尽管只输入了两个数，但是由于reg3此时也恰好为0，电路会错误地输出11
解决方法是在最后部分添加一个counter，并设置为stay at value，只有当计数到3时，电路才会有输出（这部分可以使用MUX或组合逻辑）
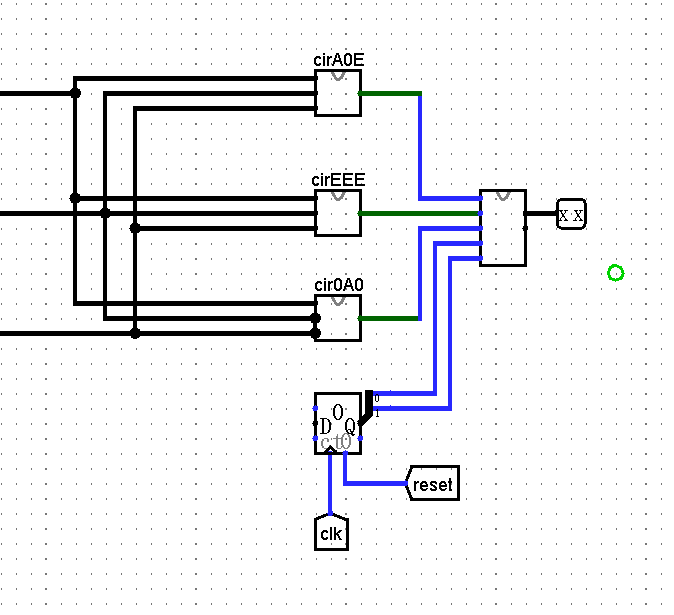输出电路(ver 2.0)
4.消除毛刺
这是本场考试我花时间最多的地方aaa~
（一些用其它方法实现的同学可以跳过此步）
上面的电路虽然看起来完善了，但是提交后并不能够通过（似曾相识www）
原因是：我的reset接在了counter上，这样就可以将counter异步复位的同时将输出清零，想法是好的，但是这样的组合逻辑清零方式会导致毛刺的出现，使清零有一个很小的延迟，让oj认为电路没有正确清零
解决方法：让reset清零时会将输出也清零
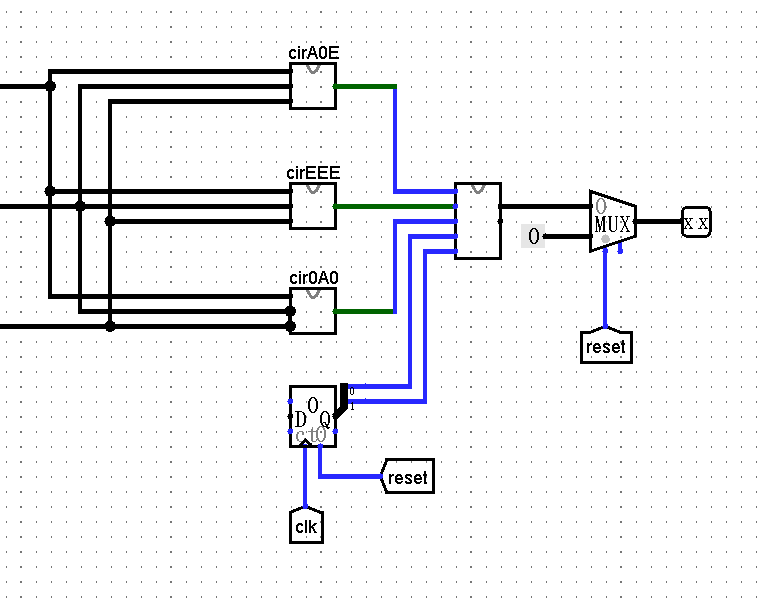输出电路(ver 3.0)
提交 通过！
不得不说，从这道题中我确实体会到了很多思想，有所长进www
法二
这是另一位佬的做法：
1.这个题可以2位控制输入，4位控制状态，然后通过多路选择器确定输入与原状态
输入 A O E X(X代表无效字符) X 00 A 01 0 10 E 11 状态 X 0000 A 0001 0 0010 E 0011 A0 0100 0A 0101 EE 0110 A0E 0111 0A0 1000 EEE 1001 2.模拟出所有state0情况下，面对不同输入的new state
右上的小选择器需要10个，每个对应一种state0（这里只画了state0=0000的情况）， 4路对应4种In
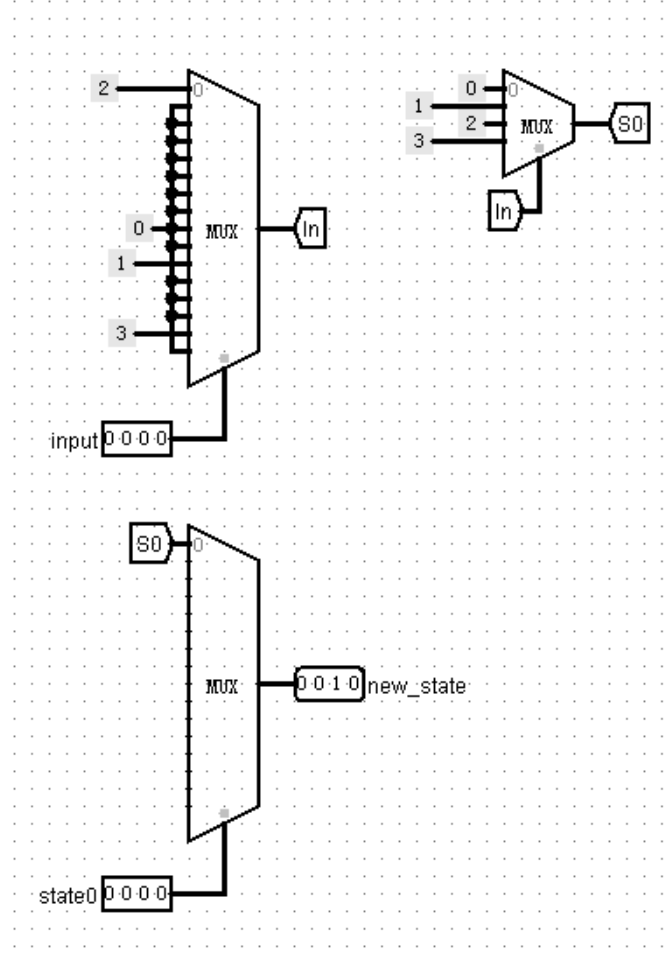
3.根据state打表得到输出
